Schalter unterschiedlich geschaltet
In diesem Abschnitt sehen Sie zwei Schaltungen. Jede der Schaltung hat zwei Schalter (A und B). Wenn ein Schalter gedrückt wird, dann werden wir dies mit einer 1 kennzeichnen, wird er nicht gedrückt, vermerken wir dies mit einer 0.
Schaltung 1
In dieser Schaltung müssen beide Schalter gleichzeitig gedrückt werden, damit die Glühlampe (G) leuchtet (G = 1), ansonsten leuchtet sie nicht (G=0). Wir können alle vier Kombinationen der Schalter und deren Einfluss auf das Leuchten der Glühlampe in einer Tabelle darstellen:
| A | B | G |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Beide Schalter sind logisch miteinander verknüpft. Diese logische Verknüpfung nennen wir UND bzw. auf Englisch „AND“.
Auch in der Aussagenlogik kennt man diese Verknüpfung. Dann stehen A, B und G für Aussagen, z.B.
- Aussage A: „Das Essen wurde von den Essensfrauen in die Theken gestellt.“
- Aussage B: „Der Laptop der Essensfirma funktioniert.“
- Aussage G: „Man kann sich Essen nehmen.“
Ferner denken wir uns statt der 0 ein „falsch“ (oder engl. „false“) und statt der 1 ein „wahr“ (oder engl. „true“).
Auch hier sind A und B mit einem AND verknüpft: Es gibt nur Essen, wenn die Aussagen A und B wahr sind (A = true, B = true). Wenn das Essen in der Theke steht (A = true), aber der Laptop nicht funktioniert (B = false), gibt es kein Essen (G = false). Genauso gibt es kein Essen (G = false), wenn zwar der Laptop funktioniert (B = true), aber das Essen noch nicht in der Theke steht (A = false). Steht kein Essen in der Theke (A = false) und funktioniert der Laptop nicht (B = false), kann es auch kein Essen geben (G = false).
Diese Verknüpfung mit der Aussagenlogik findet sich in der Bezeichnung für die obige Tabelle wieder: Wahrheitstabelle.
Zur Erinnerung: Computer arbeiten mit Transistoren, die nichts anderes sind als kleine Schalter.
Sind aber noch andere Schaltungen möglich? Sehen wir mal:
Schaltung 2
Sehen Sie sich doch mal diese Schaltung an:
Ergänzen Sie in der Spalte G der Wahrheitstabelle, ob die Glühlampe brennt.
| A | B | G |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Klicken Sie auf die Box, um die Lösung anzuzeigen!
LÖSUNG
| A | B | G |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Wird einer der beiden Schalter gedrückt, leuchtet die Glühlampe. Die Glühlampe leuchtet nur dann nicht, wenn kein Schalter gedrückt wurde. Diese Verknüpfung von A und B nennt man ODER (engl. „OR“). Man achte darauf, dass wir im Alltag manchmal das ODER benutzen, wenn wir eigentlich „entweder-oder“ meinen: „Wir dein Blinddarm heute oder morgen entfernt?“ In diesem Fall sind zwei Operationen keine Option.
Eine letzte Schaltung, mit nur einem Schalter
Wir haben noch eine letzte Schaltung, die wir analysieren können:
Hier ist jetzt ein Öffner verbaut, d.h., wenn der Schalter A nicht gedrückt wird (A = 0, A = false), leuchtet die Glühlampe (G = 1, G = true). Betätigt man aber den Öffner (A = 1, A = true), leuchtet die Glühlampe nicht (G = 0, G = false). Die Eingabe von A wird also negiert. Deswegen nennen wir die logische Verknüpfung mit der Wahrheitstabelle:
| A | G |
| 0 | 1 |
| 1 | 0 |
auch NEGATION bzw. NICHT (vom engl. „NOT“).
Logische Verknüpfungen als Bauteile: Gatter
Logischen Verknüpfungen gibt es als integrierte Schaltkreise, die als „Gatter“ bezeichnet werden. Als Bauelemente gibt es für jedes Gatter auch Schaltzeichen. Im Unterricht verwenden wir die Symbole nach dem Standard IEC 60617-12. Diese brauchen Sie noch nicht in Ihre Unterlagen zu übernehmen.
Das UND-Gatter ist nach dem Standard so definiert:
Die beiden Eingänge (in den obigen Schaltungen zu UND und ODER als die Schalter A und B dargestellt) befinden sich links, der Ausgang befindet sich rechts.
Wird also an dieses Bauteil sowohl an den oberen als auch an den unteren Eingang eine Spannung angelegt, kann man am Ausgang relativ zur Masse eine Spannung abgreifen.
Besonderheit der Simulationssoftware logic.ly
Zur Simulation von Schaltungen verwenden wir eine Software namens logic.ly. Diese Software verwendet andere Schaltzeichen für Gatter, den US-amerikanischen Standard ANSI 91-1984. Jedoch sollten Sie keine allzu großen Probleme haben, mit dieser Software umzugehen.
Formelzeichen / logische Notation
Zur Darstellung von logischen Verknüpfungen verwenden wir Formelzeichen. Sind A und B logisch mit UND verknüpft, schreiben wir \(A \land B\). Bei einer logischen Verknüpfung von A und B mit ODER, schreiben wir \(A \lor B\). Das NICHT wird durch einen Strich über der Aussagenvariable angezeigt: \(\overline{A}\)
Für diese logischen Notationen gibt es eine Eselsbrücke: Die Symbole aus der Mengenlehre. Sehen Sie sich diese beiden Venn-Diagramme an:
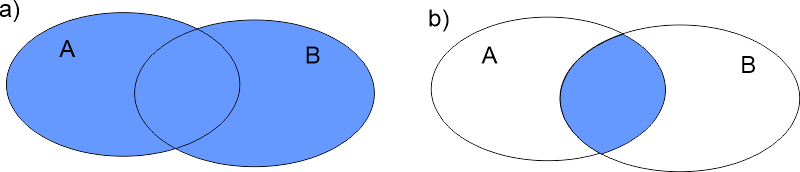
Im Fall a) ist die Vereinigungsmenge von A und B blau eingefärbt. Ein Element, das zu dieser Vereinigungsmenge gehört, gehört zu A ODER B. In der Mengenlehre würden Sie die Vereinigungsmenge so schreiben: \(A \cup B\). Schreibt man dieses Symbol etwas spitzer, erhält man \(A \lor B\).
Im Fall b) ist die Schnittmenge von A und B blau eingefärbt. Um zu dieser Menge zu gehören, muss ein Element zu A UND B gehören. In der Mengenlehre schreiben wir die Schnittmenge \(A \cap B\). Schreibt man das Symbol etwas spitzer, erhält man \(A \land B\).