Veröffentlicht von Viele physikalische Größen errechnen sich aus dem Quotienten zweier anderer Größen. Die Leistung berechnet sich zum Beispiel als Quotient der verrichteten Arbeit \(W\) in der dafür benötigten Zeit \(t\) mittels der Gleichung \(P = \frac{W}{t}\).
Manchen fällt die Umstellung solcher Gleichungen schwer. Ein einfaches Dreieck kann helfen, die Gleichungen schnell umzustellen. Hier ist das Dreieck für unser Beispiel:
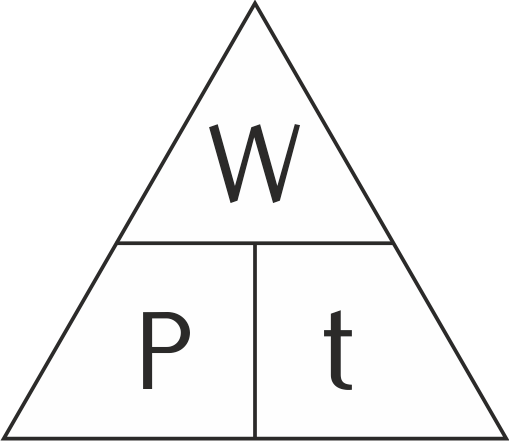
Die Verwendung des Dreiecks ist recht einfach:
- Suche die Größe, nach der du umstellen willst (z.B. \(t\)).
- Stehen die beiden anderen Größen übereinander, musst du den entsprechenden Quotienten bilden, die Größe, die im Dreieck oberhalb steht, kommt in den Zähler, die Größe, die unterhalb steht, kommt in den Nenner. In unserem Beispiel ist das \(t=\frac{W}{P}\).
- Stehen die beiden anderen Größen nebeneinander (z.B., wenn du \(W\) errechnen willst), so berechnet sich die zu berechnende Größe aus dem Produkt der beiden anderen Größen. In unserem Beispiel ist das \(W = P\cdot t\).
Hier sind Dreiecke für einige Größen.
